JuliaKara Examples

1. Particle Swarm Optimisation using JuliaKara
2. Control Kara using the keyboard
- 2.1. Problem description
- 2.2. Implementation

1 Particle Swarm Optimisation using JuliaKara

1.1 Problem description

The aim of this example is to use multiple Karas to find the region with the highest food density (leafs), in order to feed all Karas. The current density \(d\) at a location \(p\) is determined by counting all the fields in a radius \(r\) around \(p\). Therefore,

\begin{equation} d = \frac{n_{leafs}}{n_{fields}} \end{equation}

where \(n_{leafs}\) is the number of found leafs and \(n_{fields}\) is the number of total fields.

1.2 Implementation

The implementation is made based on particle swarm optimisation (PSO) ¹. Herein the velocity \(v_{i,j}\) and position \(p_{i,j}\) of a particle \(i\) (or Kara) is updated as follows:

\begin{equation} v_{i,j+1} = v_{i,j} + c_1 \cdot r_1 \cdot (p_{i,j}^{best} - p_{i,j}) + c_2 \cdot r_2 \cdot (p_{j}^{gbest} - p_{i,j}) \end{equation} \begin{equation} p_{i,j+1} = p_{i,j} + v_{i,j+1} \end{equation}

where \(j\) denotes the current step, \(p_{i,j}^{best}\) denotes the best known position for particle \(i\), \(p_{j}^{gbest}\) denotes the globally best known position, \(c_1\) and \(c_2\) are learning factors an usually \(c_1 = c_2 = 2\) and \(r_1\) and \(r_2\) are random numbers uniformly distributed between 0 and 1.

However, two problems arise:

The best known points change as karas, of course, eat the leafs they find
In this world Karas should only be able to move one step per iteration

Therefore, an alternative implementation based on PSO is derived in Section 1.3.

1.3 Solution

1.3.1 Startup

To startup JuliaKara it is loaded and for convenience some additional methods are imported

using JuliaKara
import JuliaKara.JuliaKara_noGUI.ActorsWorld:Location,
Orientation,
location_fix_ooBound,
actor_definition_at_location,
Actor

import JuliaKara.JuliaKara_noGUI.ACTOR_DEFINITIONS

1.3.2 Initialise the World

The world's size is defined by the following variables:

const world_width = 50
const world_height = 50

Initially the world is created empty.

world = World(world_width,world_height,"PSO Kara")

Fill the world with random leafs

The leaf distribution is generated such that the world consists of large, medium and small sized spots. Therefore, two functions are defined which generate random points withing the world and random sizes relative to the world's size.

"Returns a random points withing the word of size world_width x world_height"
function randP()
    Location(rand(1:world_width),rand(1:world_height))
end

"""
Returns a randomises size relative to the world
The function takes the smalles dimension and mutliplies it with the desired
relative size with a small randomisation.
"""
function randS(relSize::Float64)
    s = convert(Int,round(
        min(world_width,world_height)*(relSize + relSize*rand())
    ))
    return max(s,1)
end

Define the parameters for generating the areas of leaf. The leaf areas (combination of random location and random size) are stored in a Tuple where the first index is the location and the second index is the size.

# Number of leaf areas
n_big = 1
n_medium = rand(5:10)
n_small = rand(20:30)
# Size of leaf areas
points=[
    [(randP(),randS(0.15)) for _ in 1:n_big]...,
    [(randP(),randS(0.03)) for _ in 1:n_medium]...,
    [(randP(),randS(0.005)) for _ in 1:n_small]...
]

Draw the leaf areas as circles using the radius p[2].

for p in points
    # Iterate of all possible coordinates from -r to +r in x and y direction.
    for dx in -p[2]:p[2], dy in -p[2]:p[2]
        # Catch errors which occour when placing leafs above each other
        try
            # Check if the current location is within the circle
            if dx^2+dy^2 <= p[2]^2
                # The location is obtained by adding the dx and dy to the
                # coordinate stored in p[1].
                loc_fix = location_fix_ooBound(
                    world.world,Location(p[1].x+dx,p[1].y+dy)
                )
                # Place a leaf at the calculated location.
                JuliaKara.JuliaKara_noGUI.place_leaf(world.world,loc_fix.x,loc_fix.y)
            end 
        end
    end
end

# Redraw the world
JuliaKara.world_redraw(world,true)

The code above generates the random world of leafs shown in Figure 1.

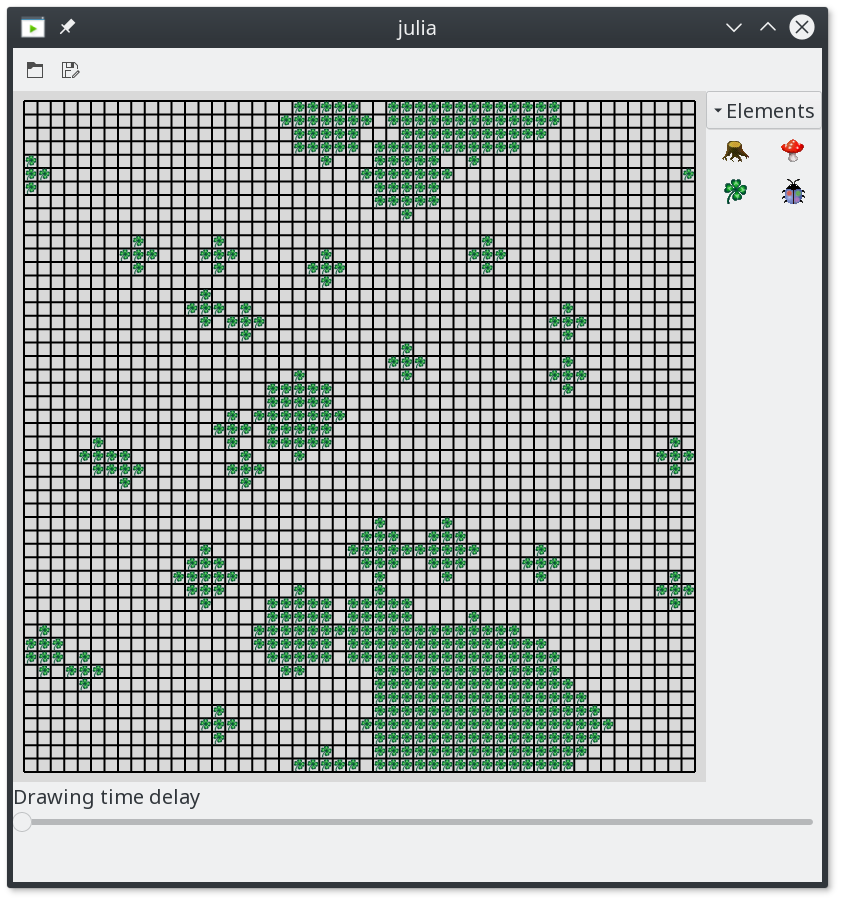
Figure 1: 50x50 World filled with random areas of leafs

1.3.3 Searching Algorithm

As described in Section 1.2 the "quality" of a location is determined by its density, meaning the ration of leafs and empty fields around the location.

"The function returns the current leaf density at location p"
function density_at(world::JuliaKara.World_GUI,p::Location,r::Int)
    # Number of leafs
    c_leafs = 0
    # Iterated of all possible positions within -r and +r in x and y
    for dx in -r:r, dy in -r:r
        # Calculate the location by adding dx and dy to p.
        pos = location_fix_ooBound(world.world,Location(p.x+dx,p.y+dy))
        # Check if there is a leaf at the position
        if actor_definition_at_location(world.world,pos,ACTOR_DEFINITIONS[:leaf]) 
            c_leafs += 1
        end
    end
    # The number of total fields is (2*r+1)
    return c_leafs / (2r+1)^2
end

One of the problems mentioned in Section 1.2 is that the Karas eat the leafs they find. Therefore, it is difficult to implement the exact PSO algorithm as \(v_{i,j}\), \(p_{i,j}^{best}\) and \(p_{i,j}^{gbest}\) change in every iteration. Hence, for this implementation \(v_{i,j}\) is neglected for the step \(j+1\), \(p_{i,j}^{best}\) is assumed to the location of a (random) field around kara with a leaf and \(p_{i,j}^{qbest}\) is the currently best density.

To obtain \(p_{i,j}^{best}\) a function next_leaf is defined as follows.

"The functions returns the movement (dx,dy) needed to reach a leaf."
function next_leaf(world::JuliaKara.World_GUI,p::Location)
    # Shuffle the list of possible dx,dy movements around the current position to
    # always return a different one.
    for dp in shuffle([(1,0),(-1,0),(0,1),(0,-1),(-1,1),(1,1),(1,-1),(-1,-1)])
        # Calculate the location
        pos = location_fix_ooBound(world.world,Location(p.x+dp[1],p.y+dp[2]))
        # Only take this location if a leaf and no other kara is there.
        if (actor_definition_at_location(world.world,pos,ACTOR_DEFINITIONS[:leaf])
            && !actor_definition_at_location(world.world,pos,ACTOR_DEFINITIONS[:kara]))
            return dp
        end
    end
    # If no possible location was found return the current.
    return (0,0)
end

In each iteration the Karas are updated by means of the implementation described in Section 1.2.

function update_kara!(world::JuliaKara.World_GUI,kara::Actor,p_gbest::Location)
    # Parameters for the PSO
    c_1,c_2,r_1,r_2 = 50,2,rand(),rand()
    # Relativ movement to the next leaf as tuple
    dL = next_leaf(world,kara.location)
    # Relative movement to the currently highest density as tuple
    dGg = ((p_gbest.x - kara.location.x), (p_gbest.y - kara.location.y))
    # Ceck if moving out at one side of the world is faster than moving across
    dGg = (
        abs(dGg[1]) > world_width/2 ? -sign(dGg[1])*(world_width-abs(dGg[1])) : dGg[1],
        abs(dGg[2]) > world_height/2 ? -sign(dGg[2])*(world_height-abs(dGg[2])) : dGg[2],
    )
    # Velocities or relative movements for the next step
    # Round and convert to integer, as kara can only move by single fields
    dx = convert(Int,round(c_1 * r_1 * dL[1] + c_2 * r_2 * dGg[1]))
    dy = convert(Int,round(c_1 * r_1 * dL[2] + c_2 * r_2 * dGg[2]))
    # At this point it is possible that dx and/or dy are 0.
    # Therefore to prevent stagnation pick a random direction.
    dx = dx==0 ? rand([-1,1]) : dx
    dy = dy==0 ? rand([-1,1]) : dy
    # Perform the movement under the restriction of only moving one field into x
    # and y. 
    if dx<0
        # Turn west
        while kara.orientation != Orientation(:WEST)
            turnLeft(world,kara)
        end
        move(world,kara)
    elseif dx>0
        # Turn east
        while kara.orientation != Orientation(:EAST)
            turnLeft(world,kara)
        end
        move(world,kara)
    end
    if dy<0
        # Turn south
        while kara.orientation != Orientation(:SOUTH)
            turnLeft(world,kara)
        end
        move(world,kara)
    elseif dy>0
        # Turn north
        while kara.orientation != Orientation(:NORTH)
            turnLeft(world,kara)
        end
        move(world,kara)
    end
    # If Kara is on a leaf ... eat it!
    if onLeaf(world,kara)
        removeLeaf(world,kara)
    end
end

As all Karas within the world need an update in the iteration another method is defined which updates a vector of Karas. In some cases it is possible that the maximum density is reached at multiple locations, therefore, the desired maximum is picked randomly from the list of multiple karas.

function update_kara!(world::JuliaKara.World_GUI,karas::Vector{Actor})
    # All current densities
    dens = [density_at(world,pi.location,2) for pi in karas]
    # The maximum density
    dens_max = maximum(dens)
    # All indices where the maxmimum density occured
    dens_inds = filter(i->dens[i]==dens_max,1:length(karas))
    # Iterate over all karas
    for (i,kara) in enumerate(karas)
        # If kara itself is contained in the maximum densites then take this
        # location
        ind = i in dens_inds ? i : shuffle(dens_inds)[1]
        # Update this kara
        try
            update_kara!(world,
                         kara,
                         karas[ind].location
                         )
        end
    end
end

The number of Karas to be placed in the world is defined by the following variable.

number_of_karas = 20

Place the Karas at random positions.

# Store all Karas in a vector
karas = Actor[]
sizehint!(karas,number_of_karas)
for i in 1:number_of_karas
    # Generate a random positon
    loc = randP()
    # Place Kara there if no other Kara is placed there.
    while actor_definition_at_location(world.world,loc,ACTOR_DEFINITIONS[:kara]) 
        loc = randP()
    end
    # Add kara to the list of karas and place in, facing north, into the world.
    push!(karas,place_kara(world,loc.x,loc.y,:NORTH))
end

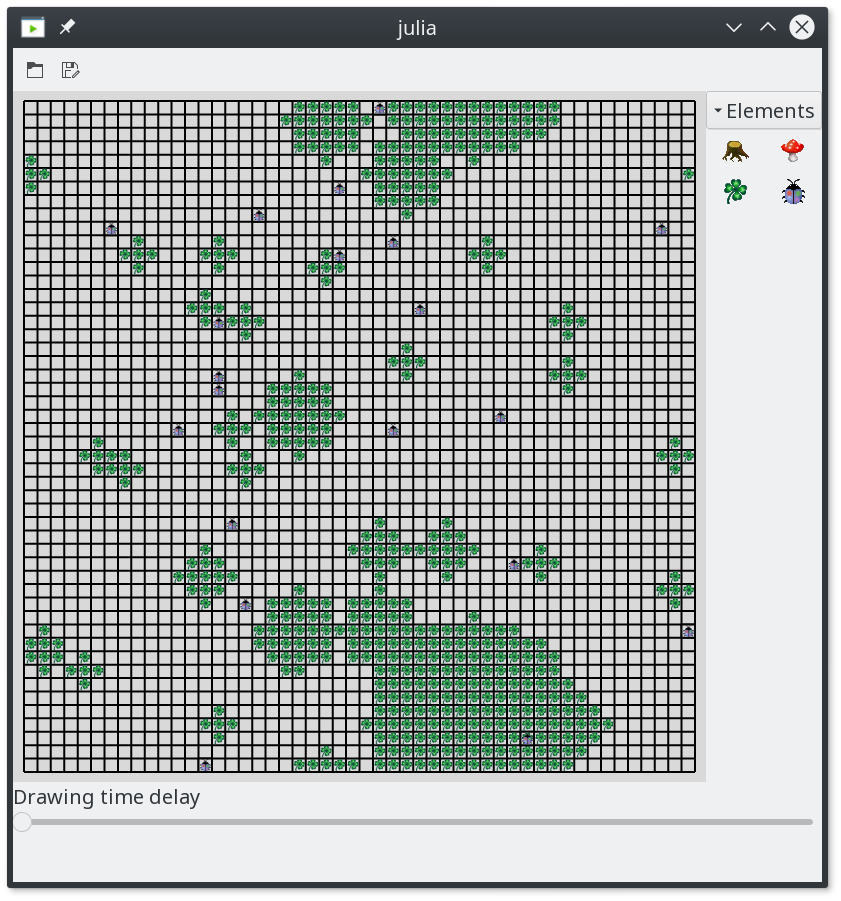
Figure 2: Starting positions of 20 Karas

Run the optimisation for 500 steps.

for i in 1:500
    update_kara!(world,karas)
end

Figure 3: Karas start to eat

2 Control Kara using the keyboard

2.1 Problem description

The aim of this example is to enable keyboard controls for Kara. The arrow keys shall be used to

move forward,
turn right and
turn left.

l shall be used to place or remove a leaf.

2.2 Implementation

To startup JuliaKara it is loaded and for convenience some additional methods are imported. Furthermore to connect signal to functions and events Gtk is loaded.

using JuliaKara
using Gtk
using Gtk.ShortNames
import JuliaKara.JuliaKara_noGUI.Actor

The world is initialised as follows.

@World (10,10)

To allow connection of various worlds (windows) to the contained Karas the function kara_keybinding is defined which brings world and kara into a local scope to the returned function which actually performs the desired operations.

The possible operations are defined in a dictionary named actions.

function kara_keybinding(world::JuliaKara.World_GUI,kara::Actor)
    function (widget,event)
        actions = Dict( 
            Gtk.GdkKeySyms.Up => ()->move(world,kara),
            Gtk.GdkKeySyms.Left => ()->turnLeft(world,kara),
            Gtk.GdkKeySyms.Right => ()->turnRight(world,kara),
            Gtk.keyval("l") => function ()
                if onLeaf(world,kara)
                    removeLeaf(world,kara)
                else
                    putLeaf(world,kara)
                end
            end 
        )
        if event.keyval in keys(actions)
            actions[event.keyval]()
        end
    end
end

To connect the defined function the function signal_connect is used, which binds the function returned from kara_keybinding to the key-release-event ².

id = signal_connect(
    kara_keybinding(world,kara),
    world.window,
    "key-release-event"
)

Now it's possible to move Kara using the arrow keys and place and remove leafs using l.

Footnotes:

http://www.swarmintelligence.org/tutorials.php

https://developer.gnome.org/gtk3/stable/GtkWidget.html#GtkWidget-key-release-event